この記事は 【AtCoder】初中級者が解くべき過去問精選 100 問を緑色コーダーが C++ で解いてみた の子記事です。お読みになる前に親記事をご確認ください。
累積和について 元記事 でも紹介されている下記の記事が参考になります。
76. 全国統一プログラミング王決定戦本戦 A – Abundant Resources
N \leq 3000 であるため、連続する区画を全探索し、愚直に区画の資源埋蔵量の総和を計算すると計算量は \Omega(N^3) = 10^{10} 程度です。実行時間制限に違反しそうです。
区画 i から 区画 i + k – 1 までの k 個の資源埋蔵量の総和を \mathrm{dp}[k][i] とおきます。以下の更新式を立式できます。
\mathrm{dp}[k + 1][i] = \begin{cases}
\mathrm{dp}[k][i] + A_{i + k}&(i + k \leq N) \\
0&(i + k > N)
\end{cases}
上記の動的計画法を実行後、\max_i \mathrm{dp}[k][i] を計算すれば、答えが得られます。
動的計画法に O(N^2), k ごとの最大値の算出に O(N^2) かかるため、全体の計算量は O(N^2) = 10^7 程度になり、実行時間制限を満たして解答できます。
区間 [1, i) の資源埋蔵量の総和を C_i とおきます。C_i は以下の漸化式を使って O(N) で計算できます。
C_{i + 1} = C_{i} + A_i
C_1, C_2, \dots, C_{N + 1} をあらかじめ用意しておくと区画 i から 区画 i + k – 1 までの k 個の資源埋蔵量の総和は C_{i + k} – C_i と O(1) で計算できます。
C_1, C_2, \dots, C_{N + 1} を使って連続する区画を全探索したとき、計算量は O(N^2) となり、実行時間制限に違反せずに解答できます。
77. JOI 2010 本選 1 – 旅人
i 日目の移動のたびに宿場町 k から宿場町 k + a_i までの距離を計算する場合、計算量は \Omega(mn) = 10^{10} 程度になります。実行時間制限に違反しそうです。
宿場町間の距離の累積和をあらかじめ計算する場合、計算量は O(m + n) = 10^6 程度になり、実行時間制限を満たして解答できます。
10^5 で割った余りを答える問題ですが、累積和の計算の際は 10^5 の剰余を計算する必要はありません。n \leq 10^5, s_i \leq 100 より累積和の値は 10^7 以下であるためです。剰余の累積和ではなく、元の値の累積和の場合、距離の計算に絶対値が使えるため多少実装が楽になります。
78. JOI 2011 本選 1 – 惑星探査
K 個の調査領域ごとに都度、「ジャングル」「海」「氷」を数え上げる場合、計算量は \Omega(KMN) = 10^{11} 程度になり、実行時間制限に違反しそうです。
累積和を何も考えずに書けるようにする! の「4. 二次元累積和」に記載の二次元累積和という手法を使うことを考えます。
以下の前処理を行うと二次元累積和を適用できそうです。
- 北西 (1, 1) 南東 (i, j) の長方形の領域内にある「ジャングル」の個数の表を作成します。
- 北西 (1, 1) 南東 (i, j) の長方形の領域内にある「海」の個数の表を作成します。
- 北西 (1, 1) 南東 (i, j) の長方形の領域内にある「氷」の個数の表を作成します。
前処理に O(MN), 各調査領域に対し O(1) の計算量がかかります。全体の計算量は O(MN + K) = 10^7 程度です。実行時間制限を満たして解答できます。
79. AtCoder Beginner Contest 106 D – AtCoder Express 2
クエリのたびに M 本の列車を確認する場合、計算量は \Omega(MQ) = 10^{10} 程度になり、実行時間制限に違反しそうです。
N \leq 500, Q \leq 100000 であるため、O(NQ) = 10^8 程度です。1 クエリを O(N) で計算する方法を考えます。
c[L][R] を都市 L から都市 R までの区間を走る列車の本数とします。a[L][R] は バケットソート のバケットと同様に O(M) で計算できます。
S[p][q] を、都市 p から都市 q までの区間に、走る区間が完全に含まれる列車のうち、走る区間の西の端が都市 p である列車の本数とします。p を固定すると、S[p][q] は c[p][q] の累積和とみなせるため、以下の式を使って O(N^2) で S[p][q] を計算できます。
S[p][q] = \begin{cases}
0&(p>q) \\
c[p][q]&(p = q) \\
c[p][q] + S[p][q – 1]&(p<q)
\end{cases}
クエリ (p_i, q_i) に対し、S[p][q] についての以下の式を使うと、完全に含まれる列車の本数を O(N) で計算できます。
\sum_{j=p_i}^{q_i} S[j][q_i]
全体の計算量は O(M + N^2 + NQ) = 10^8 程度です。制限時間以内に解答できます。
AtCoder の解説 にあるように、二次元累積和を使うとより高速に答えを求められます。
\hat{S}[p][q] を区間 [0, p) にある都市から区間 [0, q) にある都市までの区間を走る列車の本数とします。累積和を何も考えずに書けるようにする! の「4. 二次元累積和」に記載の方法で \hat{S}[p][q] を O(N^2) で計算できます。
クエリ (p_i, q_i) に対し、\hat{S}[p][q] についての下記の式を使うと、完全に含まれる列車の本数を O(1) で計算できます。
\hat{S}[q + 1][q + 1] – \hat{S}[p][q + 1] – \hat{S}[q + 1][p] + \hat{S}[p][p]
全体の計算量は O(M + N^2 + Q) になります。
80. GigaCode 2019 D – 家の建設
すべての長方形に対し、愚直に土地代と家の建設費を計算する場合、計算量は \Omega(H^3W^3) = 10^{12} 程度になり、実行時間制限に違反しそうです。
二次元累積和を使って土地代を計算する場合、1 つの土地に対し、O(1) で土地代と家の建設費を計算できます。全体の計算量は O(H^2W^2) = 3 \times 10^8 程度です。以下の解答例では制限時間内に解答できていますが、違反について判断しにくい計算量です。もう少し計算量を減らすことを考えます。
土地の縦の座標 (第何行か第何行まで) を固定したとき、購入できる土地のうち、横幅が最大の土地が面積最大の土地です。このことから二次元累積和としゃくとり法を組み合わせると、1 つの縦の座標に対し、購入できる土地の面積の最大値を計算量 O(W) で探索できます。しゃくとり法については下記の記事が参考になります。
具体的には、縦の座標を固定し、左端を第 i 列に固定したとき、第 j 列を右端とする土地は購入でき、第 j + 1 列を右端とする土地は購入できないことが分かったとします。この場合、左端を第 i + 1 列に固定したときには右端の探索を第 j + 2 列から始めてよいです。なぜなら、i \leq k \leq j + 1 となる k について、第 i + 1 列を左端、第 k 列を右端とする土地の大きさは第 i 列を左端、第 j 列を右端とする土地の大きさ以下だからです。左端、右端ともに各列 1 回ずつしか探索しないため、計算量は O(W) となります。
全体の計算量は O(H^2 W) = 10^7 程度となり、実行時間制限に違反せずに解答できます。
81. AtCoder Beginner Contest 014 C – AtColor
灰色の濃さのバケットに対し、アンケートごとに区間 [a, b] に 1 を加えて、濃さごとの購入希望客数の最大値を求める方法では、計算量が \Omega(n) \times 10^6 = 10^{11} 程度になり、実行時間制限に違反しそうです。
本問題はいもす法の典型問題です。いもす法 の「いもす法の基本: 1 次元 0 次いもす法」に類題の解説があります。以下のように対応付けて、いもす法を用いると、O(n) = 10^6 程度の計算量で解答できます。
| いもす法のイメージ図 | 類題 | 本問題 |
|---|---|---|
| 横軸 | 時刻 | 灰色の濃さ |
| 縦軸 | 入店客数 | 購入希望客数 |
82. AOJ 2013 – 大崎
1 日の時刻 (秒単位) のバケットに対し、時刻表記載の列車ごとに発時刻から着時刻までの区間に 1 を加えて、同時に必要な電車の本数を調べる方法では、計算量が 24 \times 60 \times 60 \times O(n) 程度となります。問題文に n についての制約が記載されていないため、この解法で実行時間制限に違反するか調べたところ、違反しませんでした。
いもす法を使って各時刻で必要な電車の本数を調べる場合は計算量は O(n) + 24 \times 60 \times 60 程度になります。n だけでなく、データセットの件数も不明であるため、見積はできませんが、解答例 1 が時間内に計算できるため、いもす法でも求解できます。
83. JOI 2015 本選 1 – 鉄道運賃
鉄道を利用するたびに切符で乗車するか、IC カードで乗車するかを場合分けして探索する場合、計算量は \Omega(2^{MN}) です。実行時間制限に違反しそうです。
問題文の以下の記述に着目します。
一度購入した IC カードは,何度でも使用することができる.
IC カードで乗車する場合の運賃の方が紙の切符で乗車する場合の運賃よりも安い.すなわち,i = 1, 2, \dots, N−1 に対して,A_i > B_i が成り立つ.
旅行中に一度でも IC カードで乗車する鉄道 i には常に IC カードで乗車した方が運賃の和を少なくできることがわかります。このことから、各鉄道について、以下のいずれかの場合のみ考えれば十分です。
場合 1 常に切符で乗車する場合
場合 2 常に IC カードで乗車する場合
上記の場合を探索するときの計算量は O(2^N) です。まだ実行時間制限に違反しそうです。各鉄道ごとにいずれの場合が安いのか調べる方法を考えます。
IC カードの購入費 C_i 円を帳消しにできるほど鉄道を利用する回数が多い場合は IC カードを購入した方が良さそうです。旅行を通して鉄道 i を利用する回数を n_i とします。常に切符で乗車する場合と常に IC カードで乗車する場合について、それぞれの鉄道 i の運賃と IC カード購入費用の合計は以下のように立式できます。
場合 1 A_i n_i
場合 2 B_i n_i + C_i
よって、各鉄道の利用回数が分かれば、各鉄道の運賃と IC カード購入費用の合計の最小値がわかります。各鉄道の利用回数はいもす法を使うと O(M + N) で計算できます。
各鉄道の運賃と IC カード購入費用の合計の最小値の和が答えであるため、全体の計算量は O(M + N) = 10^6 程度です。実行時間制限を満たして解答できます。
84. JOI 2012 本選 4 – 釘
正三角形を囲む輪ゴムごとに内側の釘に印を付けて、最後に釘の個数を数える場合、計算量は \Omega(M N^2) = 10^{13} 程度になります。実行時間制限に違反しそうです。
いくつかのクエリ (輪ゴム) によって塗り潰される (囲われる) 領域を計算するため、いもす法を検討します。いもす法が実行しやすいように正三角形に並んだ釘に以下の 3 つの変更を行います。
- 各釘を左に平行移動して、右側の辺が斜辺となる直角二等辺三角形に変形します。
- 左の辺の左側と底辺の下側に、辺と並行に釘を打ち、1 辺を N + 2 に拡大します。元の直角二等辺三角形の座標は変わらないように、座標は (0, 0) から始めます。
- 各釘を叩いて伸ばして同じ大きさの正方形のマスにします。
例えば、N = 5 の場合の正三角形を変形すると以下の図形になります。赤枠が新たに追加した釘に対応します。
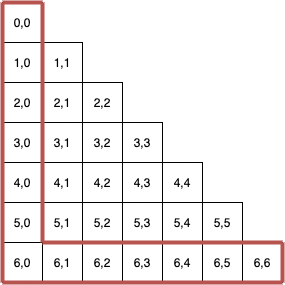
2 次元の長方形のいもす法のときは以下のように 1 と -1 を加えて左から右に累積和、上から下に累積和を計算します。
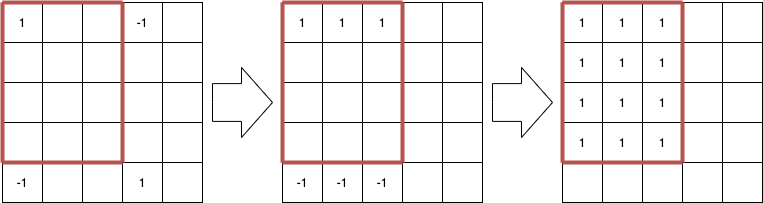
この問題でも同様に各輪ゴムの正三角形 (変形後は直角二等辺三角形) の頂点の周囲に 1 と -1 を加えて、各方向の累積和を計算することで、直角二等辺三角形を塗りつぶせないか考えます。
まず、最後の累積和を計算する前の 1 と -1 を考えます。例えば、以下のように 1 と -1 を配置できれば、上から下に累積和を計算することで赤枠の図形を塗りつぶせます。

上図では 1 が斜めに、-1 が横に並んでいます。そこで、左右の累積和と斜めの累積和を計算することで、上記の配置になる 1 と -1 の配置を検討します。試行錯誤が必要ですが、以下のように 1 と -1 を配置し、左から右の累積和、右下から左上への累積和を計算すると上図の 1, -1 の配置になります。

クエリ (赤枠の図形) に対して 1 と -1 が必ず配置できるように縦横ともに N + 2 個のマスを確保しておくことに注意します。
以下に計算手順をまとめます。
- 大きさ (N + 2) \times (N + 2) のグリッドを用意し、各マスの値を 0 とします。
- 輪ゴムごとに上図のように 3 箇所のマスを +1 し 3 箇所のマスの値を -1 します。
- 右から左、右下から左上、上から下の順に累積和を計算します。
- 値が 1 以上のマスを数えます。
それぞれの計算量は順に、O(N^2) (vector のコンストラクタのリファレンス 参照), O(M), O(N^2), O(N^2) です。全体の計算量は O(M + N^2) = 10^8 程度になり、実行時間制限に違反せずに計算できます。
JOI の解説 にあるように動的計画法でも解答できます。
\mathrm{dp}[i][j] を以下の満たす最大の正三角形 (釘 1 本の場合も含みます) の 1 辺を成す釘の本数とします。
- 釘 (i, j) を上の頂点とします。
- ある 1 本の輪ゴムによって、三角形内のすべての釘は囲われています。
どの輪ゴムも (i, j) の釘を囲わない場合は \mathrm{dp}[i][j] = 0, (i, j) の釘を囲う輪ゴムが、左下、右下のいずれかの釘を囲わない場合は \mathrm{dp}[i][j] = 1 とします。
もし、\mathrm{dp}[i][j] が分かれば、\mathrm{dp}[i][j] \geq 1 となる釘の本数が答えになります。
\mathrm{dp}[i][j] は (0, 0) の釘から帰納的に計算できます。より具体的には \mathrm{dp}[i][j] は以下の値の最大値になります。
値 1 0
値 2 釘 (i, j) を上の頂点とする輪ゴムの正三角形のうち、最大の正三角形の 1 辺を成す釘の本数
値 3 \mathrm{dp}[i – 1][j – 1] – 1
値 4 \mathrm{dp}[i – 1][j] – 1
以下は \mathrm{dp}[i – 1][j – 1] = 4, \mathrm{dp}[i – 1][j] = 3 のときの 3, 4 のイメージ図です。
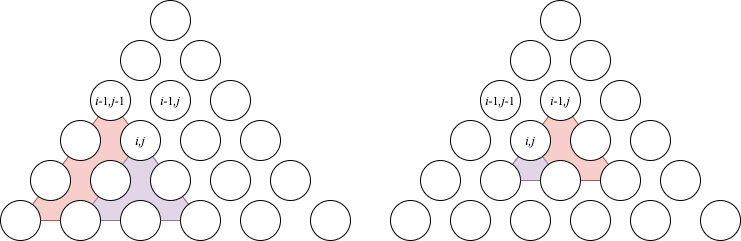
そのため、\mathrm{dp}[i][j] は以下の初期化と更新を行うことで計算できます。
初期化
\mathrm{dp}[i][j] を (i, j) を上の頂点とする輪ゴムの正三角形のうち、最大の正三角形の 1 辺を成す釘の本数で初期化します。条件を満たす正三角形が存在しない場合は 0 で初期化します。
更新
\mathrm{dp}[i + 1][j + 1] =
\max(\mathrm{dp}[i][j] – 1, \mathrm{dp}[i][j + 1] – 1, \mathrm{dp}[i + 1][j + 1])
計算量は初期化に O(M), 更新に O(N^2), 計数に O(N^2) かかるため、全体の計算量は O(M + N^2) です。
