この記事は 【AtCoder】初中級者が解くべき過去問精選 100 問を緑色コーダーが C++ で解いてみた の子記事です。お読みになる前に親記事をご確認ください。
5. AtCoder Beginner Contest 095 C – Half and Half
A ピザ、B ピザ、AB ピザを買う枚数を列挙する場合、計算量は \Omega(XY \max(X, Y)) = 10^{15} 程度になり、実行時間制限に違反しそうです。
A ピザ、B ピザ、AB ピザについて、どれかのピザの買う枚数が決まると残りのピザの買う枚数も決まらないか考えます。(実際はどれでもよいのですが) 対称性を考慮して AB ピザを買う枚数が決まるときに残りのピザの枚数が決まらないか考えます。
Z を AB ピザを買う枚数とします。A ピザ, B ピザともに Z/2 (小数点以下切り捨て) 枚用意できます。X \leq Z / 2 のとき、A ピザの追加の購入は不要です。X > Z/2 のときは X – Z/2 枚追加で購入します。場合分けをまとめると \max(0, X – Z/2) 枚の A ピザを追加で買います。同様に B ピザは \max(0, Y – Z/2) 枚、追加で買う必要があります。そのため、このときの費用は以下の式のように表せます。
A \max(0, X – Z / 2) + B \max(0, Y – Z / 2) + C Z
AB ピザを全く買わない場合から、全て AB ピザでまかなう場合まで、つまり 0 \leq Z \leq 2 \max(X, Y) の範囲で Z を変えながら、費用の最小値を探索すれば答えが求まります。
計算量は O(\max(X, Y)) = 10^5 程度で実行時間制限を満たして解答できます。
計算量 O(1) で解く場合は次のように考察して解きます。
A ピザを 1 枚用意する方法は A ピザを 1 枚買うか、AB ピザを 2 枚買うかの 2 通りです。もし、A が 2C より高い場合は、AB ピザを 2 枚買った方が費用を抑えられます。A = 2C のときは A ピザについての費用は同じですが、B ピザも 1 枚用意できることから AB ピザを 2 枚買った方が良さそうです。
B ピザ 1 枚を用意する方法についても同様です。
A ピザ 1 枚と B ピザ 1 枚を用意する方法は A ピザ B ピザを 1 枚づつ購入する方法 (A + B 円) と AB ピザを 2 枚購入する方法 (2C 円) の 2 通りあります。このときに用意できるピザは A ピザ 1 枚 B ピザ 1 枚と同じであるため、単純に A + B と 2C を比較して、安い方法を採用すれば良さそうです。
以上をもとに、場合分けを 2C の数直線にまとめます。場合分けの際 A \leq B とします。A \geq B の時は A と B をひっくり返して A \leq B の時と同様に考えれば良いためです。

場合 1 2C \leq A \ ( \leq B) のとき
A ピザを用意するにしろ、B ピザを用意するにしろ、AB ピザを 2 枚用意する方がお得です。AB ピザの購入枚数は 2\max(X,Y) 枚です。AB ピザを 2 枚購入すると、A ピザ 1 枚、B ピザ 1 枚用意できるため、X と Y のうち多い方の 2 倍の枚数の AB ピザを購入すれば十分だからです。
場合 2 A \leq 2C \leq B のとき
B ピザは AB ピザを購入して用意します。B ピザの用意のために AB ピザを 2Y 枚購入した際、A ピザも Y 枚用意できるため、X > Y の時は Y – X 枚 A ピザを用意すれば十分です。A<2C のため、A ピザを X – Y 枚購入します。ここで \max(0, X – Y) 枚購入すると考えておくと、X \leq Y の場合も考慮でき、場合分けが減らせます。
場合 3 (A \leq) B \leq 2C \leq A + B のとき
A ピザ B ピザとも、少なくとも \min(X, Y) 枚までは用意する必要があるため、2\min(X, Y) 枚 AB ピザを購入します。X > Y の時は X – Y 枚 A ピザを購入し、Y > X の時は Y – X 枚 B ピザを購入します。これも、それぞれ \max(0, X – Y) 枚、\max(0, Y – X) 枚購入すると考えると、場合分けを減らせます。
場合 4 A + B<2C のとき
単に A ピザを X 枚、B ピザを Y 枚購入するのが最も安く済みます。
4 つの場合の費用を下記の式で計算できます。
場合 1 2C\max(X, Y)
場合 2 2CY + A\max(0, X – Y)
場合 3 2C\min(X, Y) + A\max(0, X – Y) + B\max(0, Y – X)
場合 4 AX + BY
あとは if 文を使って場合分けをすれば答えが求まります。
A > B の時は swap 関数を使って、A と B, X と Y の値を入れ替えると A \leq B の場合のコードが利用できます。
if (A > B) {
swap(A, B);
swap(X, Y);
}
6. 三井住友信託銀行プログラミングコンテスト 2019 D – Lucky PIN
N 個の数字から 3 つの数字を取り出す組み合わせは {}_N C _3 通りです。\Omega(N^3) = 10^{12} 程度の計算量の解法だと、実行時間制限を超える見積になるため、組み合わせを全て確認するのは難しそうです。
3 桁の数字の組み合わせ (0 から始まっても良い) は 1000 通りです。n (0 \leq n \leq 999) が設定されうる暗証番号か否かの判定は以下のようにできます。S[i] を S の左から i 番目の文字とします。
- 添字 j を 1 から 3 まで順に変えながら、以下を繰り返します。
- 添字 i を i_{j-1} + 1 で初期化します。(i_{0} = 0 とします)
- 暗証番号の候補 n の左から j 桁目の数字と S[i] が一致するまで、i を 1 大きくします。
一致したときの i を i_j とおきます。
一致する i が存在しない場合、n は設定されうる暗証番号ではありません。
- 添字 i_1, i_2, i_3 が存在するとき、S[i_1]S[i_2]S[i_3] は n に一致するため、n は設定されうる暗証番号です。
上記の判定は O(N) で実行できます。全体の計算量は 1000 \times O(N) = 10^8 程度で実行時間制限を満たして解答できます。
S[i] を順番に見ていき、i 番目までの状況を元に i + 1 番目までの数字を使って作成できる暗証番号の候補を計算する方法もあります。
S[:i] を S の左から 1 番目から i – 1 番目までの文字列とします。
暗証番号の候補のうち、S[i] が暗証番号の末尾である候補は S[:i] から i – 3 桁を消して残りの 2 桁を左から読んだ文字列の末尾に S[i] を加えたものになります。各 i に対し、S[:i] をラッキーナンバーとした 2 桁版暗証番号の候補が分かれば i を 1 \leq i \leq N の間で変えながら、暗証番号の候補を列挙すれば答えが得られそうです。
S をラッキーナンバーとする 2 桁版暗証番号の候補について考えます。
2 桁版暗証番号の候補のうち、S[i] が末尾である候補は S[:i] から i – 2 桁を消して残りの 1 桁を左から読んだ文字列の末尾に S[i] を加えたものになります。各 i に対し、S[:i] をラッキーナンバーとした 1 桁版暗証番号の候補が分かれば、2 桁版暗証番号の候補の列挙もできそうです。
1 桁版暗証番号の候補については、各 S[i] を確認すれば良いです。
U_{1,i} を S[:i] をラッキーナンバーとした際の 1 桁版暗証番号の候補の集合とします。同様に U_{2,i}, U_{3,i} を定義します。
これまでの考察から i について以下の漸化式が成り立ちます。
\begin{aligned}
U_{3,i+1} &= U_{3,i} \cup \{tS[i] \ | \ t \in U_{2,i}\} \\
U_{2,i+1} &= U_{2,i} \cup \{tS[i] \ | \ t \in U_{1,i}\} \\
U_{1,i+1} &= U_{1,i} \cup \{S[i]\}
\end{aligned}
上記は暗証番号を文字列とみなす場合の漸化式ですが、整数としてみる場合は s_i を S[i] の整数へのキャストとすると次の通りです。
\begin{aligned}
U_{3,i+1} &= U_{3,i} \cup \{10t + s_i \ | \ t \in U_{2,i}\} \\
U_{2,i+1} &= U_{2,i} \cup \{10t + s_i \ | \ t \in U_{1,i}\} \\
U_{1,i+1} &= U_{1,i} \cup \{s_i\}
\end{aligned}
i を 1 から N まで順に変えながら、上記の漸化式で U_{1,i}, U_{2,i}, U_{3,i} を計算すれば、U_{3, N+1} が暗証番号の候補の集合になります。
i ごとの漸化式の更新の計算は、バケットソート のバケットを使う場合、set を使う場合のどちらでも U_{3,i+1} 計算時の t \in U_{2,i} のループが計算がボトルネックになります。ただ、U_{2, i} の要素数は高々 100 のため、高速に計算できます。
全体の計算量は 100 \times O(N) = 10^7 程度で実行時間制限を違反せずに解答できます。
バケットを bitset を使って管理することも可能です。
ビット演算がしやすいように U_{1,i}, U_{2,i}, U_{3,i} の更新を i を N から 1 まで降順に変えながら行います。このとき漸化式は以下のようになります。
\begin{aligned}
U_{3,i-1} &= U_{3,i} \cup \{t + 100 s_i \ | \ t \in U_{2,i}\} \\
U_{2,i-1} &= U_{2,i} \cup \{t + 10 s_i \ | \ t \in U_{1,i}\} \\
U_{1,i-1} &= U_{1,i} \cup \{s_i\}
\end{aligned}
U_{1,i} がビット列で表現されているとき、\{t + 10 s_i \ | \ t \in U_{1,i}\} は U_{1,i} を 10 s_i だけ左にシフトさせると求められます。同様に \{t + 100 s_i \ | \ t \in U_{2,i}\} もビット演算で求められます。
U_{3,0} が暗証番号の候補の集合になります。
計算量は 1000 \times O(N) = 10^8 程度ですが、ビット演算は高速であるため、実際の計算時間は上記の解答例 1 と同程度には高速な実装が可能です。
7. JOI 2007 本選 3 – 最古の遺跡
4 つの柱の組み合わせを試すのは \Omega(n^4) = 10^{14} となり、実行時間制限の 3 秒以内には終わりそうにありません。
平面上の正方形は四隅の座標のうち 2 つの座標が分かれば残りの座標の候補 (2 つの候補があります) も計算できます。このうち 1 つの候補の計算方法を考えます。
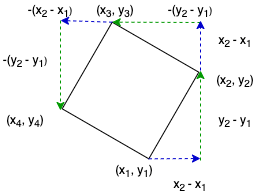
座標 (x_1, y_1), (x_2, y_2) が与えられた時、合同な三角形の性質から残りの座標 (x_3, y_3), (x_4, y_4) は以下のように計算できます。
\begin{aligned}
x_3 = x_2 – (y_2 – y_1), \quad&y_3 = y_2 + (x_2 – x_1) \\
x_4 = x_1 – (y_2 – y_1), \quad&y_4 = y_1 + (x_2 – x_1)
\end{aligned}
そのため、2 つの柱の組み合わせごとに、神殿になるか((x_3, y_3), (x_4, y_4) に柱があるか) を確認し、神殿になる場合は面積を計算して、最大値を記録すれば解答できます。神殿になるかの判定は、柱を set に入れておけば O(\log(n)) でできますし、5001 \times 5001 のバケットを用意すれば O(1) でできます。全体の計算量はそれぞれ O(n^2 \log n), O(n^2) で共に間に合います。
正方形の面積は三平方の定理から下記の式で求められます。
(x_2 – x_1)^2 + (y_2 – y_1)^2
先ほど、2 点 ((x_1, y_1), (x_2, y_2)) が与えられたとき、正方形の残りの四隅の候補は 2 つあると述べました。もう 1 つの候補は (x_2, y_2) から (x_1, y_1) に向かう反時計回りに (x_3, y_3), (x_4, y_4) があるような (上図だと右下に残りの 2 点があるような) 候補です。この候補については調べる必要がありません。もし、2 つめの候補の (x_3, y_3), (x_4, y_4) に柱がある場合、はじめに紹介した候補の計算方法により 2 つの柱の組み合わせ (x_3, y_3), (x_4, y_4) に対し、(x_1, y_1), (x_2, y_2) を残りの座標として導出し、面積を計算するためです。言い換えると神殿が成立する場合ははじめに紹介した方法で 2 つめの候補も列挙できており、神殿が成立しない場合はそもそも列挙しなくてよいためです。
