【AtCoder】「分野別　初中級者が解くべき過去問精選 100 問」解答例【逆元を使う問題】

この記事は【AtCoder】初中級者が解くべき過去問精選 100 問を緑色コーダーが C++ で解いてみたの子記事です。お読みになる前に親記事をご確認ください。

$10^9 + 7$ などの数で割ったときの余りを出力させる問題で逆元の計算が必要になることがあります。このような問題に不慣れな方は元記事で紹介されている下記の記事を読むとよいかもしれません。

「1000000007 で割ったあまり」の求め方を総特集！〜逆元から離散対数まで〜

AtCoder Library の Modint には $\Z / p \Z$ 上の逆元を計算量 $O(\log p)$ で計算するメンバ関数 inv があります。逆元が必要な場合は inv を使って問題を解きます。また除算 / (逆元との乗算) も同じ計算量で計算できます。こちらも使います。

72. AtCoder Beginner Contest 034 C – 経路
73. AtCoder Beginner Contest 145 D – Knight
74. AtCoder Beginner Contest 021 D – 多重ループ
75. AtCoder Beginner Contest 149 F – Surrounded Nodes

72. AtCoder Beginner Contest 034 C – 経路

問題へのリンク

$H + W$ 回のマス目の移動を下記の $2$ 通りで場合分けして列挙し、 $(W, H)$ に到着するかを判定する場合、計算量は $\Omega(2^{H + W})$ となり、実行時間制限に違反しそうです。

マス $(i, j)$ からマス $(i + 1, j)$ への移動
マス $(i, j)$ からマス $(i, j + 1)$ への移動

隣接するマス目からの移動を考慮した動的計画法を用いても $\Omega(HW) = 10^{10}$ 程度の計算量になり、制限時間を超えそうです。

この問題は高校数学の単元「場合の数と確率」の典型的な問題です。下記の記事に解説がありますが、この問題の答えは ${}_{H + W – 2} C_{W – 1}$ となります。

【数A場合の数】最短経路の求め方どうしてＣを使うの？

${}_{H + W – 2} C_{W – 1}$ は下記のように $W - 1$ 回の加算、 $2 W - 2$ 回の乗算と $1$ 回の除算で計算できます。

${}_{H + W – 2} C_{W – 1} = \frac{\prod_{i = 1}^{W – 1} (i + H – 1)}{\prod_{i = 1}^{W – 1} i} = \frac{H(1 + H) \cdots (W + H – 2)}{1 \cdot 2 \cdots (W – 1)}$

Modint のドキュメントによると modint1000000007 の加算・乗算は $O(1)$ , 除算は $O(\log \mathrm{mod})$ ( $\mathrm{mod}$ は剰余算の法、この問題では $10^9 + 7$ ) で計算できます。全体の計算量は $O(W) = 10^5$ 程度となり、実行時間制限を満たして解答できます。

解答例

73. AtCoder Beginner Contest 145 D – Knight

問題へのリンク

問題 72 と同様に、ビット全探索の場合 $\Omega(2^{X + Y})$ , 動的計画法の場合 $\Omega(XY) = 10^{12}$ 程度の計算量になるため、これらの解法では実行時間制限に違反しそうです。

ナイトの駒の $1$ 回の移動方法は下記の $2$ 通りです。

マス $(i, j)$ から $(i + 1, j + 2)$ への移動
マス $(i, j)$ から $(i + 2, j + 1)$ への移動

これらはそれぞれ、元の位置ベクトルにベクトル $(1, 2)$ , $(2, 1)$ を加えた位置ベクトルへの移動と考えられます。ベクトルの加法は可換であるため、移動方法の組み合わせ (正確には重複順列) に対し、移動方法 1 と 2 の順番を入れかえても到着するマスは変わりません。例えば、入力例 1 出力例 1 の移動は移動方法 1 と 2 からなる重複順列 1, 2 と 1 と 2 を入れ替えた重複順列 2, 1 の列挙とみなせます。

原点 $(0, 0)$ から $(X, Y)$ にナイトの駒を移動させるとき、移動方法 1 を使う回数を $a$ , 移動方法 2 を使う回数を $b$ とします。これは位置ベクトル $(0, 0)$ にベクトル $(1, 2)$ を $a$ 回、ベクトル $(2, 1)$ を $b$ 回足した位置ベクトル $(a + 2b, 2a + b)$ への移動とみなせます。移動先は $(X, Y)$ のため、以下の連立方程式が立式できます。

$\begin{cases} a + 2b = X \\ 2a + b = Y \end{cases}$

これを $a, b$ について解くと $a = (2Y - X) / 3$ , $b = (2X - Y) / 3$ となります。 $a, b$ は非負の整数のため、以下の場合には答えは $0$ となります。

場合 1 　 $X>2Y$ または $2X<Y$ の場合 ( $a$ または $b$ が負となる場合)
場合 2 　 $2Y - X$ または $2X - Y$ が $3$ の倍数でない場合 ( $a$ または $b$ が整数でない場合)

上記以外の場合には $a + b$ 回の移動のうち、移動方法 1 を $a$ 回使う移動の場合の数 $\left( {}_{a + b} C_a \right)$ が答えになります。

${}_{a + b} C_a$ は $a$ 回の加算、 $2 a$ 回の乗算と $1$ 回の除算で計算できます。AtCoder Library の Modint の modint1000000007 を使う場合、これらの計算量はそれぞれ $O(1)$ , $O(1)$ , $O(\log \mathrm{mod})$ ( $\mathrm{mod}$ は剰余算の法、この問題では $10^9 + 7$ ) です。全体の計算量は $O(a) = O(Y) = 10^6$ 程度になり、実行時間制限を満たして解答できます。

解答例

74. AtCoder Beginner Contest 021 D – 多重ループ

問題へのリンク

for ループのネストの深さが $2$ の場合のプログラムの計算量は $\Omega(n^2) = 10^{10}$ 程度です。 $k \geq 2$ の場合には愚直にプログラムを作成すると実行時間制限に違反しそうです。

$1 \leq a_1 \leq a_2 \leq \cdots \leq a_k \leq n$ であるような整数の組 $(a_1, a_2, \cdots, a_k)$ の個数は重複組み合わせという考え方を使って立式できます。重複組み合わせについては下記の記事が参考になります。

重複組合せの公式と例題（玉，整数解の個数）

$a_0 \coloneqq 1, a_{k + 1} \coloneqq n, x_i \coloneqq a_{i} – a_{i – 1}$ とおくと $\{x_i\}_{i=1}^{k + 1}$ と $\{a_i\}_{i=0}^{k + 1}$ は一対一に対応し、以下が成立します。

$\begin{aligned} \begin{cases} x_i \geq 0 \quad (1 \leq i \leq k + 1)\\ \sum_{i = 1}^{k + 1} x_i = n – 1 \end{cases} \iff \begin{cases} a_{i – 1} \leq a_i&(1 \leq i \leq k + 1) \\ 1 \leq a_i \leq n&(1 \leq i \leq k) \\ \end{cases} \end{aligned}$

このことをふまえて以下の問題を考えます。

$\sum_{i = 1}^{k + 1} x_i = n – 1$ という方程式について非負整数解の個数を求めよ。

上記の記事の例題 3 の解説をもとに問題を解くと答えは ${}_{k + n – 1} C_k$ となります。先ほど確認した対応から ${}_{k + n – 1} C_k$ は $1 \leq a_1 \leq a_2 \leq \cdots \leq a_k \leq n$ であるような整数の組 $(a_1, a_2, \cdots, a_k)$ の個数です。つまり、元の問題の剰余を計算する前の答えです。

${}_{k + n – 1} C_k$ は $k$ 回の加算、 $2 k$ 回の乗算と $1$ 回の除算で計算できます。AtCoder Library の Modint の modint1000000007 を使う場合、これらの計算量はそれぞれ $O(1)$ , $O(1)$ , $O(\log \mathrm{mod})$ ( $\mathrm{mod}$ は剰余算の法、この問題では $10^9 + 7$ ) です。全体の計算量は $O(k) = 10^5$ 程度になり、実行時間制限を満たして解答できます。

解答例

75. AtCoder Beginner Contest 149 F – Surrounded Nodes

問題へのリンク

$T$ の各頂点の白黒のパターンを列挙する場合、 $\Omega(2^{N})$ の計算量になります。実行時間制限に違反しそうです。

期待値の式を変形して、すべての場合を列挙せずに計算する方法を探します。

白を $0$ , 黒を $1$ として $x \in \{0, 1\}^N$ を $T$ の頂点 $i$ の色が $x_i$ である塗り方とします。 $S_{x}$ を塗り方 $x$ のときの $S$ とします。 $I_U$ を集合 $U$ の指示関数とします。言い換えると $I_U$ を $i\in U$ なら $I_U(i) = 1$ , $i \notin U$ なら $I_U(i) = 0$ である関数とします。
塗り方 $x$ のときの穴あき度は $x_{i} = 0$ かつ $i \in S_{x}$ である $i$ の個数であるため、以下のように立式できます。

$\sum_{i = 1}^{N} I_{\{j | x_j = 0\}} (i) I_{S_{x}} (i)$

よって求める期待値 $E$ は以下のように立式・式変形できます。

$E = \sum_{x \in \{0, 1\}^N} \left( \sum_{i = 1}^{N} I_{\{j | x_j = 0\}} (i) I_{S_{x}} (i) \right) 2^{-N} = 2^{-N} \sum_{i = 1}^{N} \left( \sum_{x \in \{0, 1\}^N} I_{\{j | x_j = 0\}} (i) I_{S_{x}} (i) \right)$

上記の式変形から各頂点 $i$ に対し、 $x_i = 0$ かつ $i \in S_{x}$ となる $x$ の個数が分かれば $E$ を計算できます。

入力例 4 について、頂点 $1$ を $T$ の根と考え、頂点 $7$ に着目します。

上記は頂点 $7$ を根とする部分木に属さない頂点の集合を青色、 $7$ の子 ( $2$ と $4$ ) を根とする部分木をそれぞれ、緑色、赤色のグループに分けています。

青緑赤のグループのうち、少なくとも $2$ グループに黒色の頂点が属するとき、またそのときにかぎり、頂点 $7$ は $S$ に属します。グループが異なる黒色の頂点を繋ぐために $7$ を経由する必要があるからです。
包除原理を考えると頂点 $x_7 = 0$ かつ、 $7 \in S_{x}$ となる塗り方 $x$ の個数はすべての塗り方 ( $2^7 = 128$ ) から以下の塗り方の個数を引くことで計算できます。

塗り方 1 　頂点 $7$ を黒にする塗り方
塗り方 2 　頂点 $7$ を白に塗り、黒に塗られる頂点が青緑赤のいずれか $1$ グループにのみ属する塗り方
塗り方 3 　すべての頂点を白にする塗り方

それぞれの個数は以下の通りです。

塗り方 1 　 $2^{7 – 1} = 64$
塗り方 2 　 $(2^{2} – 1) + (2^{3} – 1) + (2^{1} – 1) = 11$
塗り方 3 　 $1$

塗り方 1, 2, 3 の計算方法を見ると、各グループの頂点の個数が分かっていれば、加算減算とべき乗で頂点 $i$ に対し $x_i = 0$ かつ、 $i \in S_{x}$ となる塗り方 $x$ の個数が計算できることがわかります。AtCoder Library の Modint の modint1000000007 を使う場合、加算減算とべき乗の計算量はそれぞれ $O(1)$ , $O(\log N)$ です。各頂点ごとに計算し、親が異なるときその子の集合どうしは互いに素であるため、全体の計算量は $O(N \log N)$ ほどになりそうです。この程度の計算量であれば、実行時間制限を満たせそうです。

実装時に混乱しないよう、計算を以下の段階に分けます。

頂点 $i$ に対し、 $i$ を根とする部分木の頂点を数えます。
頂点 $i$ に対し、 $2$ の ( $i$ を根とする部分木の頂点数) 乗を計算します。
頂点 $i$ に対し、 $2$ の ( $i$ を根とする部分木に属さない頂点の数) 乗を計算します。
頂点 $i$ に対し、上記の包除原理を使う方法で $x_i = 0$ かつ $i \in S_{x}$ となる塗り方 $x$ を数えます。
4 の結果を足し合わせて、 $2^{N}$ で割り、 $E$ を算出します。

それぞれの大まかな方法と計算量は以下の通りです。

段階	方法	計算量
1	深さ優先探索	$O(N)$
2	1 の結果とべき乗の `for` 文	$O(N \log N)$
3	1 の結果とべき乗の `for` 文	$O(N \log N)$
4	2,3 の結果と深さ優先探索	$O(N)$
5	4 の結果、加算の `for` 文と除算	$O(N + \log \mathrm{mod})$

全体の計算量は $O(N \log N + \log \mathrm{mod}) = 10^7$ 程度で、実行時間制限を満たして解答できます。

解答例 1

$2^{i + 1} = 2 \times 2^{i}$ であることをふまえて、 $2^{0}, 2^{1}, \dots, 2^{N}$ を事前に計算しておくと上記の段階 2, 3 は $O(N)$ で計算できます。

解答例 2

上記は AtCoder の解説の解法 2 に近い、頂点に着目した解法です。解法 1 の通り、辺に着目しても解答できます。

$E$ を以下のように式変形します。

$\begin{aligned} E &= \sum_{x \in \{0, 1\}^N} \left( \sum_{i = 1}^{N} I_{\{j | x_j = 0\}} (i) I_{S_{x}} (i) \right) 2^{-N} = \sum_{x \in \{0, 1\}^N} \left( \sum_{i = 1}^{N} \left(1 – I_{\{j | x_j = 1\}} (i) \right) I_{S_{x}} (i) \right) 2^{-N} \\ &= \sum_{x \in \{0, 1\}^N} \left( \sum_{i = 1}^{N} \left ( I_{S_{x}} (i) – I_{\{j | x_j = 1\}} (i) I_{S_{x}} (i) \right) \right) 2^{-N} \end{aligned}$

$x_{i} = 1$ すなわち、頂点 $i$ が黒に塗られるならば、 $i \in S_{x}$ です。そのため、 $I_{\{j | x_j = 1\}} I_{S_{x}} = I_{\{j | x_j = 1\}}$ が成り立ちます。よって、 $E$ は以下のように $S_{x}$ の頂点の個数の期待値から計算できます。

$\begin{aligned} E &= 2^{-N} \sum_{x \in \{0, 1\}^N} \sum_{i = 1}^{N} I_{S_{x}} (i) – 2^{-N} \sum_{x \in \{0, 1\}^N} \sum_{i = 1}^{N} I_{\{j | x_j = 1\}} (i) \\ &= 2^{-N} \sum_{x \in \{0, 1\}^N} \sum_{i = 1}^{N} I_{S_{x}} (i) – 2^{-N} \sum_{i = 1}^{N} \sum_{x \in \{0, 1\}^N} I_{\{j | x_j = 1\}} (i) \\ &= 2^{-N} \sum_{x \in \{0, 1\}^N} \sum_{i = 1}^{N} I_{S_{x}} (i) – \frac{N}{2} \end{aligned}$

$S$ は木であるため、 $S$ の頂点の数は $S$ の辺の数 $+ 1$ です。そこで $T$ の各辺について、 $S_{x}$ の辺となる塗り方 $x$ を数えます。

入力例 4 について、頂点 $1$ を $T$ の根と考え、辺 $(1, 7)$ に着目します。

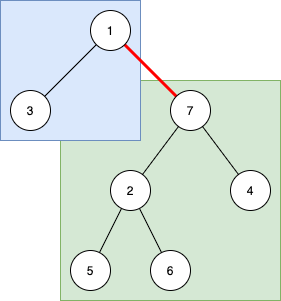
上記は辺 $(1, 7)$ を切るとできる $2$ つの連結成分をそれぞれ、青色、緑色にグループ分けしています。

両方のグループに黒色の頂点が属するとき、またそのときにかぎり、辺 $(1, 7)$ は $S$ に属します。グループが異なる黒色の頂点を繋ぐために辺 $(1, 7)$ を経由する必要があるからです。
辺 $(1, 7)$ が $S$ に属する塗り方は $(2^{2} – 1) (2^5 – 1)$ 通りあることがわかります。

頂点に着目した解法と同様に、各頂点を根とする部分木の頂点の数が分かっていれば、各辺について $S_{x}$ の辺となる塗り方 $x$ を数えることができます。

辺の個数から頂点の個数を計算する際に一点、気を付けることがあります。すべての頂点を白に塗る場合は $S = \empty$ となり、頂点の数と辺の数が一致します。そのため、辺の個数から頂点の個数を計算する際は期待値としては $1 – 2^{-N}$ , 場合の数としては $2^N - 1$ を加えることに注意してください。

計算量は $O(N \log N + \log \mathrm{mod})$ です。