【AtCoder】「分野別　初中級者が解くべき過去問精選 100 問」解答例【最小全域木問題】

ゆえに、通行料金の和が最小のとき、移動に利用する道路のグラフは全域木になります。木の場合、どの都市を開催都市として選んでも、開催都市を根として深さ優先探索の帰りがけ順に各都市の選手を親の都市に移動させることで、すべての道路の利用を $1$ 回に抑えることできます。つまり、求める最小値は開催都市に依存せず、利用する道路の通行料金の和になります。道路の通行料金の和が最小になる組み合わせは通行料金を重みとしたときの最小全域木です。これはクラスカル法で求められます。

$K > 1$ のときを考えます。
$K = 1$ のときと同様に考えると $K$ 本の木からなる全域森のうち、辺の重み (道路の通行料金) の和が最小になるものが答えになります。開催都市はそれぞれの木から $1$ つづつ選びます。以降のこの全域森を $K$ 最小全域森と呼びます。(これは造語です)

$K$ 最小全域森はクラスカル法を辺を $N - K$ 本追加したときに中断することで構成できます。Kruskal法をココロから納得するに記載の最小全域木問題の最適性条件をもとにした下記の命題を示すことでアルゴリズムの正しさを確認できます。

無向連結グラフ $G$ が与えられ、各辺 $e$ の重みを $w(e)$ とする。また $T$ を $G$ の $K$ 本の木からなる全域森とする。このとき、以下は同値である。

全域森 $T$ は $K$ 最小全域森である。
全域森 T に含まれない任意の辺 e について、以下のいずれかが成立する。
1. グラフ $T \cup {e}$ は閉路をもち、 $f \in T$ を閉路の辺としたとき $w(f) \leq w(e)$ が成立する。
2. 任意の $f \in T$ に対し、 $w(f) \leq w(e)$ が成立する。

Kruskal法をココロから納得するの最小全域木問題の最適性条件の証明方法にならって示します。

1 $\Rightarrow$ 2

対偶を示します。
以下を満たす $e \in G \setminus T$ が存在すると仮定します。

グラフ $T \cup \{e\}$ に閉路は存在しない。
グラフ $T$ に $w(f) > w(e)$ を満たす辺 $f$ が存在する。

このとき、 $(T \setminus \{f\}) \cup \{e\}$ は $K$ 本の木からなる全域森です。 $w(f) > w(e)$ より、この全域森の重みは $T$ の重みより小さいです。そのため、 $T$ は $K$ 最小全域森ではありません。

2 $\Rightarrow$ 1

$S$ を $N - K$ 本の辺からなる $G$ の部分グラフとします。 $| S \setminus T |$ についての帰納法で $T$ の重み $w(T)$ が $S$ の重み $w(S)$ 以下になることを示します。
$| S \setminus T | = 0$ のときは $|S| = |T| = N - K$ より $S = T$ が成り立つため、 $w(T) \leq w(S)$ です。
$| S \setminus T | \leq n – 1$ となる $S$ については正しいと仮定して、 $| S \setminus T | = n$ となる $S$ について示します。
$e \in S \setminus T$ を $T \cup \{e\}$ が閉路となる $S$ の辺とします。このような辺が存在しない場合、 $S$ の任意の辺の重みは $T$ の任意の辺の重み以上になるため、 $w(T) \leq w(S)$ が成立します。
$f \in T$ を $T \cup \{e\}$ の閉路の辺とします。 $\hat{S} \coloneqq (S \setminus \{e\}) \cup \{f\}$ とおくと $|\hat{S}| = N – K$ , $|\hat{S} \setminus T| = n – 1$ であるため、帰納法の仮定から $w(T) \leq w(\hat{S})$ です。また、 $w(f) \leq w(e)$ より $w(\hat{S}) \leq w(S)$ が成り立つため、 $w(T) \leq w(S)$ です。
特に $K$ 本の木からなる全域森は $N - K$ 本の辺からなる $G$ の部分グラフであるため、 $T$ は $K$ 最小全域森になります。

以上から $K>1$ の場合はクラスカル法を辺を $N - K$ 本追加したときに中断した時点の全域森の辺の重みの和が答えとなります。これは $K = 1$ の場合も含んでいることにご注意ください。

計算量は $O(M \log N) = 10^7$ 程度です。

解答例

66. AOJ 1127 – Building a Space Station

問題へのリンク

$2$ つの異なる cell を corridor で繋ぐ際、 $2$ つの cell の中心を通る直線に沿って cell の表面と表面を繋ぐのが、最短の繋ぎ方になります。
準備として二次元の場合を考えます。下図のように $2$ つの cell 及び、その中心を $A, B$ とおきます。また、 $A, B$ の表面上の点をそれぞれ $P, Q$ とおきます。

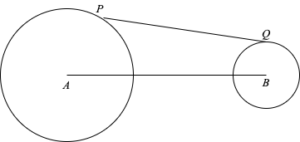
線分 $PB$ と cell $B$ の表面との交点を $R$ とします。

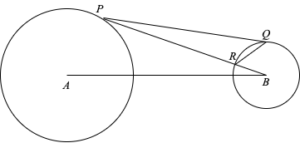
$\angle PRQ$ は $90 \degree$ 以上であるため、 $PR$ の長さは $PQ$ の長さ以下です。言い換えると $P$ を固定したとき cell $B$ の表面への最短距離は $PR$ の長さになります。
次に点 $S$ を線分 $AB$ と cell $A$ の表面との交点とします。同様に点 $T$ を線分 $AB$ と cell $B$ の表面との交点とします。

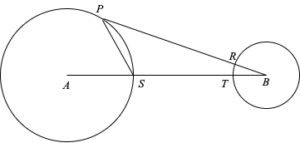
$\angle PSB$ は $90 \degree$ 以上であるため、 $SB$ の長さは $PB$ の長さ以下です。 $R$ と $T$ は共に cell $B$ の表面の点であるため、 $RB$ と $TB$ の長さは等しいです。よって $ST$ の長さは $PR$ の長さ以下です。
以上から $ST$ の長さが cell $A$ の表面から cell $B$ の表面への最短の長さになります。

三次元の場合は直線 $AB$ に $x$ 軸が一致し、点 $P$ が半平面 $\{(x, y, z) | y \geq 0, z = 0\}$ 上の点になる座標系を考えます。cell $B$ 上の点 $Q$ に対し $Q’$ を以下を満たす点とします。

点 $Q’$ は cell $B$ 上の点である。
点 $Q$ と $Q’$ の $x$ 座標は等しい。
点 $Q’$ は半平面 ${(x, y, z) | y \geq 0, z = 0}$ 上の点である。

このとき、三次元の二点間の距離を求める公式より $PQ’$ の長さは $PQ$ の長さ以下になることがわかります。 $P, Q’$ は共に $xy$ 平面上の点であるため、以降の議論を二次元の場合と同様に進められます。

以上から中心 $(x_1, y_1, z_1)$ , 半径 $r_1$ の cell と中心 $(x_2, y_2, z_2)$ , 半径 $r_2$ の cell の間を結ぶ corridor の距離の最小値は以下の式で求められます。

$\max \left(\sqrt{(x_1 – x_2)^2 + (y_1 – y_2)^2 + (z_1 – z_2)^2} – r_1 – r_2, 0 \right)$

各 cell を点、任意の点の間に上記の corrider の距離を重みとする辺が存在するグラフを考えて、クラスカル法で最小全域木の重みを求めれば答えになります。

答えは小数点以下 $3$ 桁まで表示すると指定されているため、fixed と setprecision を使って出力を調整します。

$1$ データセットに対し $O(n^2 \log n) = 10^5$ 程度の計算量で求解できます。データセットの個数は不明ですが、 $100$ 個程度なら Time Limit 以内に処理できるだろうと考えられます。

解答例

67. AtCoder Beginner Contest 065 D – Built?

問題へのリンク

すべての街と街の間に道を造る可能性を考えてクラスカル法を実行する場合、 $\Omega(N^2 \log N) = 10^{12}$ 程度の計算量になり、実行時間制限に違反しそうです。

辺 (造る道の候補) を減らすことを検討します。下記の問題文の記述から考えていきます。

座標 $(a, b)$ にある街と座標 $(c, d)$ にある街の間に道を造るのには、 $min(|a - c|, |b - d|)$ 円かかります。

最小値を求める問題のため、座標 $(a, b)$ にある街と座標 $(c, d)$ にある街の間には $|a - c|$ 円の道、または $|b - d|$ 円の道を造ることができる、と考えても同じです。
これを踏まえて、入力例 1 を見てみます。

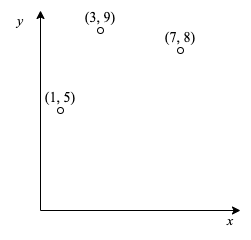
座標 $(1, 5)$ の街と座標 $(7, 8)$ の街を繋ぐ際、 $|7 - 1|$ 円の道は候補から外してよいです。同じ金額で $(1, 5), (3, 9), (7, 8)$ の街すべてを繋ぐことができるためです。下記の式変形から確認できます。

$|7 - 1| = 7 - 1 = 7 - 3 + 3 - 1 = |7 - 3| + |3 - 1|$

同様に、座標 $(1, 5)$ の街と座標 $(3, 9)$ の街を繋ぐ際、 $|9 - 5|$ 円の道は候補から外してよいです。

これを一般化すると、座標 $(a, b)$ の街に繋がる道路の候補は以下の $4$ 本に絞られます。

座標の $x$ 成分が $a$ 以下である街のうち、 $x$ 座標が最大の街との間の道路
座標の $x$ 成分が $a$ 以上である街のうち、 $x$ 座標が最小の街との間の道路
座標の $y$ 成分が $b$ 以下である街のうち、 $y$ 座標が最大の街との間の道路
座標の $y$ 成分が $b$ 以上である街のうち、 $y$ 座標が最小の街との間の道路

道路は無向であるため、道路の候補の本数を $2 (N - 1)$ 本に絞ることができます。これらの道路の費用は街を $x$ 座標、 $y$ 座標のそれぞれでソートすることで、計算量 $O(N \log N)$ で計算できます。

道路の候補の本数を $2 (N - 1)$ に絞ることができるため、 $O(N \log N) = 10^7$ 程度の計算量でクラスカル法を実行し、最小全域木のコストを計算することができます。このコストが答えになります。

解答例